
A bigger bandwidth results in a shorter and wider “bump” that spreads out farther from the centre and assigns more probability to the neighbouring values. Each kernel has a bandwidth, and it determines the width of the “bump” (the width of the neighbourhood of values to which probability is assigned). Then the “bump” at x = 1.5 is twice as big as the “bump” at x = 0.5.Įach “bump” is centred at the datum, and it spreads out symmetrically to cover the datum’s neighbouring values. A “bump” is assigned to every datum, and the size of the “bump” represents the probability assigned at the neighbourhood of values around that datum thus, if the data set contains Intuitively, a kernel density estimate is a sum of “bumps”.
Kernel density estimation pdf#
The definite integral of the PDF over its support set equals to 1.The PDF is then estimated by adding all of these kernel functions and dividing by the number of data to ensure that it satisfies the 2 properties of a PDF: Essentially, at every datum, a kernel function is created with the datum at its centre – this ensures that the kernel is symmetric about the datum. It is non-parametric because it does not assume any underlying distribution for the variable. Kernel density estimation is a non-parametric method of estimating the probability density function (PDF) of a continuous random variable. Some common PDFs are kernels they include the Uniform(-1,1) and standard normal distributions. its definite integral over its support set must equal to 1.Thus, a kernel is a function with the following properties (To my surprise and disappointment, many textbooks that talk about kernel density estimation or use kernels do not define this term.)Ī kernel is a special type of probability density function (PDF) with the added property that it must be even. I will also introduce rug plots and show how they can complement kernel density plots.īut first – read the rest of this post to learn the conceptual foundations of kernel density estimation.īefore defining kernel density estimation, let’s define a kernel.
Kernel density estimation how to#
In the follow-up post, I will show how to construct kernel density estimates and plot them in R.
Kernel density estimation series#
Today, I will continue this series by introducing the underlying concepts of kernel density estimation, a useful non-parametric technique for visualizing the underlying distribution of a continuous variable. Recently, I began a series on exploratory data analysis so far, I have written about computing descriptive statistics and creating box plots in R for a univariate data set with missing values. The second half will focus on constructing kernel density plots and rug plots in R. This first half focuses on the conceptual foundations of kernel density estimation.
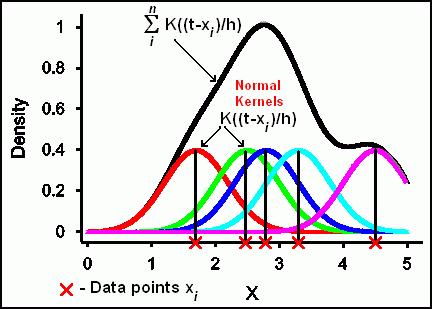
took this idea further.For the sake of brevity, this post has been created from the first half of a previous long post on kernel density estimation. Given a set of \(n\) sample points \(x_k\) ( \(k = 1,\cdots,n\)), an exact kernel densityĮstimation \(\widehat\), when the true distribution is far from Rules for an approximately optimal kernel bandwidth than it is to do so for bin width. Upon closer inspection, one finds that the underlying PDFĭoes depend less strongly on the kernel bandwidth than histograms do on bin width and it is much easier to specify One might argue that this is not a major improvement. Since KDE still depends on kernel bandwidth (a measure of the spread of the kernel function) instead of bin width, The kernel functions are centered on the data points directly, KDE circumvents the problem of arbitrary bin positioning. This kernel functions can then be summed up to get anĮstimate of the probability density distribution, quite similarly as summing up data points inside bins. That specifies how much it influences its neighboring regions. In a kernel density estimation each data point is substituted with a so called kernel function The simplest form is to create aĭensity histogram, which is notably not so precise.Ī more sophisticated non-parametric method is the kernel density estimation (KDE), which can be looked at as a sort of

Performance of univariate kernel density estimation methods in TensorFlowīy Marc Steiner from which many parts here are taken.Įstimating the density of a population can be done in a non-parametric manner. An introduction to Kernel Density Estimations, explanations to all methods implemented in zfit and a throughoutĬomparison of the performance can be found in


 0 kommentar(er)
0 kommentar(er)
